Numerical Analysis

In the Numerical Analysis research group, we focus on the development, analysis, and implementation of mathematical methods for the numerical solution of applied mathematics problems. In this context, we investigate, for example:

• Methods for numerical differentiation and integration.
• Techniques for solving (non-)linear systems of equations.

A key focus of our work is on error and convergence analysis, which ensures that the methods we develop are reliable and accurate. Furthermore, we examine structure-preserving properties of methods that maintain the physically motivated characteristics of the underlying problems (e.g. conservation of mass for incompressible fluids). An important application area is the approximation of solutions to partial differential equations (PDEs), which arise in many fields of natural and engineering sciences, such as:

• Mechanics and materials science
• Electromagnetism
• Fluid mechanics

One well-known method for the numerical approximation of PDEs is the Finite Element Method (FEM). In this approach, the domain under investigation is subdivided into smaller subdomains (e.g., triangles or tetrahedra). The following figure shows a FEM-based simulation of the magnetic field induced by a coil over a plate with a hole (team7 benchmark).  

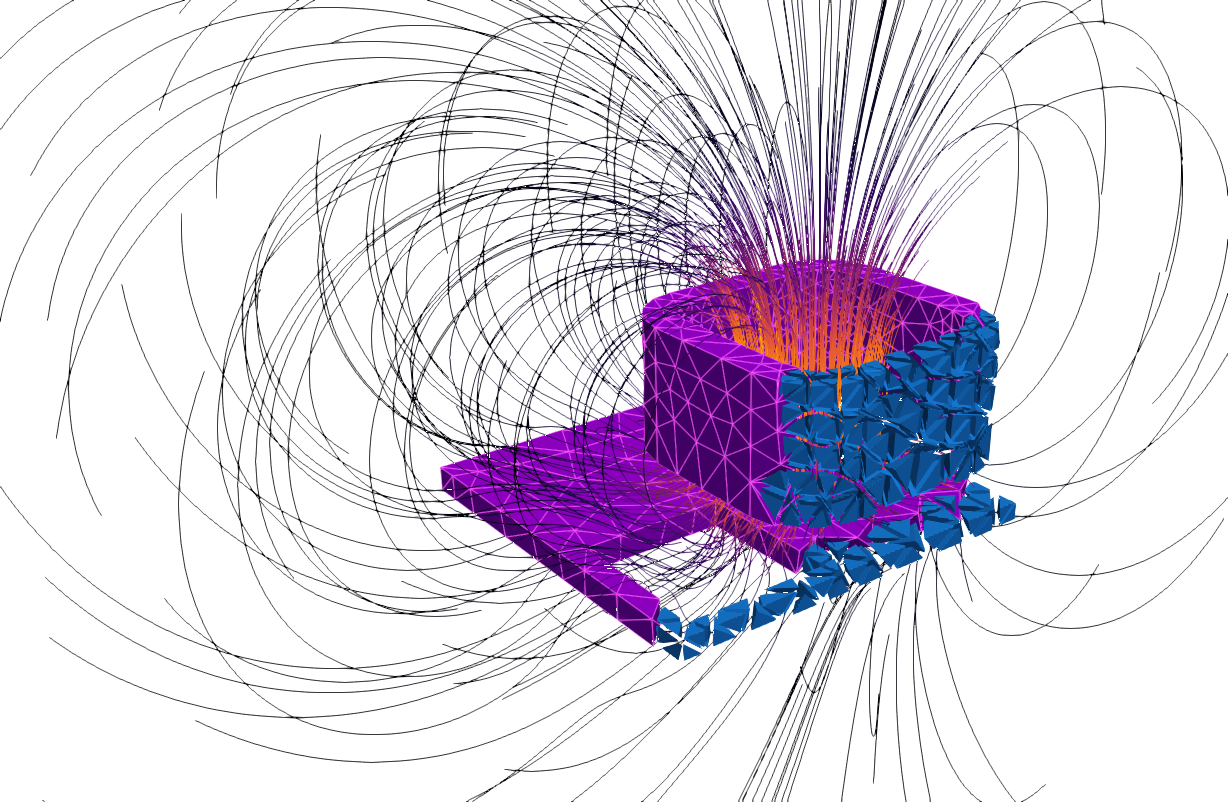
Within these subdomains, we develop FEM variants that ensure high accuracy in solutions both locally and globally. Since the number of degrees of freedom can become very large in complex problems (10⁶ and more), we also focus on the complexity analysis of algorithms. This includes, for example:

• Methods for large, sparse, or poorly conditioned matrices.
• Optimization of numerical algorithms for parallel computing architectures and supercomputers.

For practical implementation, we use open-source software such as NGSolve, which we actively employ for the implementation and analysis of our algorithms.